SYSTÈMES DE TRANSFORMATIONS (THÉORIE DES)

SYSTÈMES DE TRANSFORMATIONS (THÉORIE DES)

Élaborée dans une optique interdisciplinaire, la théorie des systèmes de transformations propose un formalisme suffisamment général pour être applicable à des champs d’investigation que l’évolution des sciences, dans son mouvement vers une spécialisation de plus en plus poussée, a séparés en disciplines distinctes. Les disciplines que cette évolution a ainsi rendues quasi autonomes, avec leurs langages propres, ont perdu de ce fait la plupart des moyens d’échanges susceptibles de les relier. Expliciter le substratum qui leur est commun, c’est rétablir la possibilité de telles connexions, dont l’histoire des sciences montre le caractère souvent très fructueux.

Précisons ce que nous entendrons par systèmes de transformations .

Définition . On dira que l’on a affaire à un système de transformations chaque fois que l’on étudiera un ensemble constitué d’éléments individualisés qui, par suite des interactions intervenant entre eux, ou des actions extérieures qui leur sont imposées, voient se modifier au cours du temps certaines au moins des caractéristiques fonctionnelles qui les définissent dans l’ensemble considéré.

On voit immédiatement que, si l’on parvient à développer un formalisme utilisable pour des systèmes définis d’une manière aussi générale, le domaine d’application possible en sera relativement étendu. Parmi les disciplines qui peuvent ainsi être regroupées, on peut citer, par exemple: la cinétique chimique ou biochimique (les objets élémentaires sont des molécules); la théorie des populations et l’écologie (les éléments sont des organismes entiers); la théorie des compartiments physiologiques (les éléments sont le plus souvent des molécules dont la fonction varie selon leur situation dans les différents organes); la théorie statistique des effets biologiques des rayonnements ou des substances chimiques, qui est l’objet d’étude de la radiobiologie, de la photobiologie, de la pharmacologie, de la toxicologie; et bien d’autres sujets où les éléments étudiés peuvent être inanimés ou vivants.

Comme on le verra au chapitre Description du formalisme , le formalisme des systèmes de transformations est présenté de manière axiomatique, mais ce mot doit être entendu dans un sens un peu différent de celui qui lui est couramment attaché en mathématiques. Le souci de rationalité interne, c’est-à-dire de cohérence des axiomes entre eux, est évidemment présent ici au même titre qu’en mathématiques. Mais les degrés de liberté que l’on peut s’accorxer dans le choix de ces axiomes sont, bien entendu, moins nombreux. L’axiomatique d’une théorie «physique», ou «naturelle», c’est-à-dire d’une théorie faite explicitement pour rendre compte de phénomènes observés , doit aussi tenir compte des liens à établir entre les concepts et grandeurs utilisés dans la théorie et les entités du monde «réel» avec lesquelles on peut les mettre en correspondance, obligation que n’ont pas les constructions de pure mathématique, ou la seule préoccupation a priori est de cohérence interne. En outre, ces correspondances que doit prendre en compte toute théorie dans les sciences naturelles ne peuvent pas être quelconques; elles doivent respecter certaines règles de réalisabilité pratique qui sont un peu plus exigeantes, en général, que le requiert la seule rationalité interne. C’est pourquoi on peut parler, à ce propos, de rationalité externe , ou d’intelligibilité . De là vient, essentiellement, que l’axiomatique d’une théorie «naturelle» ne peut pas être une construction a priori, sans contact préliminaire avec les réalités observables. Dans le cas des systèmes de transformations, l’axiomatique qui sera énoncée plus loin résulte en fait d’une synthèse inductive effectuée à partir de l’examen des situaions diverses que l’on peut rencontrer dans les disciplines qui ont été évoquées ci-dessus. Il va de soi que le champ d’application des énoncés ainsi obtenus n’est pas strictement limité aux disciplines qui ont servi de point de départ pour leur élaboration. C’est le propre de toute synthèse inductive convenablement menée que de conduire à une généralisation par rapport aux situations plus ou moins particulières d’où elle est partie. En fait, le domaine d’utilisation possible du formalisme des systèmes de transformations recouvre potentiellement tous les sujets d’étude relevant de la définition générale.

Il est enfin important de noter que le formalisme proposé reste ouvert aux extensions ou aux utilisations partielles. Les axiomes choisis ne constituent pas un carcan rigide qui devrait être utilisé en totalité dans toutes les situations. Certains systèmes, ou certaines études, peuvent ne relever que d’une partie de l’axiomatique; nous verrons, en particulier, que cela conduit à une subdivision des systèmes de transformations en quelques grands types bien définis (linéaires multiplicatifs ou non multiplicatifs, ou non linéaires). En outre, l’axiomatique actuelle peut à tout moment être étendue par l’introduction de nouveaux axiomes permettant, soit d’englober de nouveaux types de systèmes, soit de spécifier davantage (c’est-à-dire de décrire de façon plus fine) certains types plus ou moins particuliers de systèmes de transformations. On verra, par exemple, que les axiomes 3 à 7 peuvent ou non intervenir, selon que les systèmes considérés sont, ou ne sont pas, le siège des phénomènes élémentaires qu’expriment ces axiomes.

1. Description du formalisme

Axiomatique

Axiome 1 . Les objets étudiés sont considérés selon une répartition en classes d’équivalence fonctionnelle.

Cet axiome correspond au respect d’une nécessité rationnelle pour l’étude du système considéré. C’est en effet seulement lorsque cette condition est respectée qu’il est possible de considérer que tous les éléments d’une même classe sont susceptibles de subir les mêmes transformations, et chacune de celles-ci avec une même probabilité. Cette condition est nécessaire si l’on veut que le contenu de chaque classe constitue une variable «homogène» du système.

La notion de classe d’équivalence fonctionnelle peut éventuellement être assimilée à celle d’état , à condition toutefois que ce dernier terme soit appliqué à toutes les caractéristiques qui définissent le comportement des éléments dans le système considéré, et seulement à ces caractéristiques. Par ailleurs, il est important de noter que ces caractéristiques ne se limitent pas à celles qui définissent intrinsèquement les éléments, mais incluent aussi les éventuelles contraintes extérieures qui peuvent influer sur le comportement fonctionnel de ces éléments. Par exemple, deux molécules de même formule chimique, mais soumises à des contraintes spatiales différentes (l’une libre dans un récipient de réaction, l’autre adsorbée sur une paroi de ce récipient), seront considérées comme appartenant à des classes d’équivalence différentes. Pour la même raison, la situation spatiale des éléments peut éventuellement intervenir dans la définition des classes d’équivalence.

Notation utilisée:

– classe: E¹, E², ..., Eⁿ (système à n classes);

– nombre d’éléments dans chaque classe à l’instant t : N¹, ², ..., Nⁿ .

Axiome 2. Entre deux classes quelconques E^j et E^k , la possibilité de transformation peut être inexistante, à sens unique, à double sens.

Cet axiome exhaustif a pour but de réserver, dans le formalisme de base, la possibilité de toutes les structures de transformations envisageables.

Les deux premiers axiomes définissent l’ossature topologique, qualitative, du mode de description adopté. Les trois suivants sont relatifs aux différents types de transformations possibles et à l’expression analytique que l’on peut donner, pour chacun d’eux, du nombre d’objets subissant ladite transformation par unité de temps. Si l’on considère les processus fondamentaux qui peuvent être à l’origine de ces transformations, on constate qu’ils sont seulement au nombre de trois:

– Transformation ne mettant en jeu chaque fois qu’un élément, et provoquée par l’action d’une grandeur exprimable sous la forme d’un «champ» d’intensité 﨏. La notion de champ s’applique ici aux grandeurs susceptibles d’agir de la même façon sur tous les éléments d’une même classe d’équivalence; elle pourra s’appliquer à des champs au sens classique du terme (gravitationnel, électrique, magnétique, etc.), ou à des flux de particules agissant sur le système, ou à des concentrations de substances que l’on choisit de traiter sous cette forme globale (par exemple, parce qu’elles restent pratiquement constantes) plutôt que sous la forme d’un contenu variable de classe d’équivalence.

– Transformation spontanée d’un élément, due aux seules propriétés qui le définissent dans la classe d’équivalence à laquelle il appartient.

– Transformation mettant en jeu simultanément plusieurs éléments appartenant à la même classe ou à des classes différentes.

La cohérence rationnelle exige qu’une transformation issue d’une classe donnée se produise à un taux par unité de temps qui dépende du nombre d’objets présents dans cette classe puisque, en vertu de l’axiome 1, tous ces objets ont les mêmes propriétés et par conséquent les mêmes probabilités de participer à telle ou telle transformation.

De là découlent les trois axiomes suivants, dans lesquels F représente le nombre de transformations élémentaires par unité de temps.

Axiome 3. Pour une transformation E^jE^k provoquée par un champ d’intensité 﨏, on a:

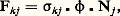靖^kj étant un facteur de proportionnalité (taux de transformation par unité de temps, pour un élément et pour un champ d’intensité unité) dépendant des classes considérées.

Axiome 4. Pour une transformation spontanée E^jE^k , on a:

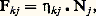兀^kj étant un facteur de proportionnalité.

Axiome 5. Pour une transformation mettant en jeu 見^j éléments de la classe E^j , 見^{j +1} éléments de la classe E^{j +1}, ..., 見^{j +p} éléments de la classe E^{j +p}, on a:

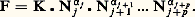F doit être indicé en fonction des classes de départ et d’aboutissement de la transformation, K est un facteur de proportionnalité.

Il est à noter que les expressions précédentes ne sont valables, en tant que moyennes de variance suffisamment faible, que dans la mesure où le nombre d’éléments dans la (les) classe(s) de départ est assez grand.

Par ailleurs, l’axiome 5, qui a la même forme que la loi d’action des concentrations de la chimie (Van’t Hoff) et que la loi des rencontres de l’écologie (Volterra), ne doit pas être considéré ici comme une relation d’origine expérimentale, et par conséquent plus ou moins approchée. On peut en effet le démontrer, comme simple loi statistique, dès que l’on admet que l’axiome 1 est respecté. Par ailleurs, il est à noter que les axiomes 3 et 4 peuvent être considérés comme des cas particuliers de l’axiome 5.

Les axiomes 3, 4 et 5 expriment les taux de transformations en fonction du contenu des classes qui sont à leur origine. Il faut encore préciser comment se traduiront ces transformations en nombre d’éléments soustraits ou apportés aux classes de départ ou d’arrivée. D’où l’axiome suivant.

Axiome 6. Une transformation E^jE^k peut, d’une manière générale, soustraire 見^kj éléments de E^j et apporter 廓^kj éléments dans E^k ( 見, 廓 entiers 閭 1).

Il est immédiat de constater que cet axiome a pour but de permettre la prise en compte de phénomènes tels que dissociation, polymérisation, dépolymérisation, multiplication, reproduction, etc.

Enfin, il faut tenir compte du fait que, pour des raisons géométriques, les contenus de certaines classes peuvent être soumis à des contraintes qui imposent entre eux le respect d’une certaine relation. C’est le cas, par exemple, de classes qui sont entre elles comme le volume et la surface d’une certain domaine de l’espace; le nombre d’éléments situés dans la classe de surface peut être imposé à chaque instant par le nombre d’éléments de la classe de volume. D’où l’énoncé général de l’axiome suivant.

Axiome 7. Certaines contraintes, en particulier de nature géométrique, peuvent imposer entre les contenus de certaines classes, et selon des cinétiques plus ou moins rapides, le respect de relations déterminées du type 﨡(N^j , N^k , ...) = 0.

Lorsque de telles relations 﨡 existeront, elles entraîneront une réduction de dimension (nombre de variables) des équations décrivant l’évolution du système. À son tour, cette réduction de dimension pourra se traduire par l’apparition dans les équations de termes (fonctions de transformations) ne satisfaisant pas aux axiomes 3, 4 et 5. Il est important de prendre en compte ce fait dans l’interprétation de tout modèle, et de ne pas oublier que l’existence de tels termes ne pourrait mettre en cause la validité des axiomes 3, 4 et 5 que s’il était prouvé qu’aucun changement de dimension du système ne peut ramener les équations à la forme canonique définie par l’axiomatique.

On trouvera dans l’article de P. Delattre «La Régulation des systèmes de transformations» (in Économie appliquée ) des exemples précis de situations dans lesquelles des taux de transformations constants (ne dépendant pas du contenu de la classe de départ), ou dépendant uniquement du contenu d’une classe différente de la classe de départ, se ramènent à l’une des formes canoniques par augmentation de dimension du système.

Représentation sous forme de graphes

Les systèmes de transformations peuvent être représentés par des graphes orientés, en vertu de la correspondance suivante établie avec les concepts classiques de la théorie des graphes:

– classes d’équivalencenœuds (ou sommets) du graphe;

– possibilités de transformationsarcs (ou liaisons orientées) du graphe.

La possibilité d’une transformation entre les classes E^j et E^k sera ainsi représentée par un schéma tel que celui de la figure 1. À l’arc E^jE^k sont associés des coefficients 見^kj et 廓^kj , ainsi que le terme F^kj exprimant le taux de cette transformation par unité de temps. Par exemple, si la transformation considérée relève des axiomes 3 ou 4, on aura l’une des formes suivantes:

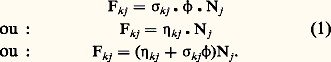Malgré la correspondance qui vient d’être définie, il est important de noter que les graphes de transformations ne peuvent pas être entièrement assimilés aux graphes classiques. Ils présentent en effet la particularité de mettre en œuvre ce que l’on peut appeler des arcs simultanés , qui correspondent aux situations où plusieurs arcs correspondent à une même transformation élémentaire. Les figures 2 et 3 illustrent deux cas de ce type, le premier correspondant à la dissociation d’un élément de la classe E¹ en 廓²¹ éléments de E² et 廓³¹ éléments de E³; le second à une association de 見³¹ éléments de E¹ et 見³² éléments de E² donnant naissance à un élément de la classe E³.

Il résulte des situations de ce genre que les graphes de transformations sont d’un maniement plus délicat que les graphes classiques, où l’on considère que tous les arcs sont indépendants.

La possibilité de représenter les systèmes de transformations par des graphes orientés permet déjà de dégager un certain nombre de propriétés très générales, de nature topologique, avant même toute étude analytique des équations qui régissent ces systèmes.

Résumons brièvement ces propriétés, après avoir rappelé quelques définitions classiques de la théorie des graphes, ainsi qu’une définition nouvelle:

– on appelle chemin dans un graphe une succession d’arcs, l’extrémité terminale de l’un d’eux correspondant au même sommet que l’extrémité initiale du suivant;

– on appelle composante d’un graphe un ensemble de sommets et des arcs qui existent entre ces sommets ;

– on appelle composante fortement connexe (C.F.C.) une composante telle qu’entre deux quelconques de ses sommets E^j et E^k il est possible de trouver un chemin E^jE^k et un chemin E^kE^j ;

– on appelle composante fortement connexe maximale (C.F.C.M.) une composante fortement connexe qui ne peut constituer, par l’adjonction d’autres composantes adjacentes, une nouvelle composante fortement connexe.

On remarquera que la définition de la composante de graphe ne fait intervenir que les arcs situés entre les sommets qu’elle comporte, alors que l’attribution du caractère fortement connexe maximal à une composante donnée implique la prise en compte des arcs qui traversent sa frontière et la relient aux autres composantes voisines. Pour améliorer la cohérence des définitions, il est donc utile d’adjoindre aux définitions classiques précédentes la définition complémentaire suivante:

– on appellera graphe vrai (GV) une composante fortement connexe maximale, y compris les arcs qui traversent sa frontière.

Compte tenu de cette définition, on voit immédiatement que, eu égard au sens des arcs qui traversent leur frontière, il ne peut exister que quatre types de graphes vrais:

– le graphe exotrope vrai (GExV), dont la frontière n’est traversée que par des arcs divergents (fig. 4 a);

– le graphe endotrope vrai (GEnV), dont la frontière n’est traversée que par des arcs convergents (fig. 4 b);

– le graphe mixte vrai (GMV), dont la frontière est traversée à la fois par des arcs divergents et par des arcs convergents (fig. 4 c);

– le graphe fermé vrai (GFV), dont la frontière n’est traversée par aucun arc (fig. 4 d).

Dans ces figures, la composante intérieure à la frontière peut être quelconque (nombre de classes et d’arcs), à la seule condition d’être fortement connexe.

En utilisant les définitions précédentes, on démontre facilement (cf. P. Delattre, L’Évolution des systèmes moléculaires et in Journ. of Theoretical Biology ):

– que tout système non fortement connexe est décomposable en graphes vrais des quatre types décrits ci-dessus;

– que cette décomposition est telle que l’intersection entre deux graphes vrais quelconques est toujours vide du point de vue des classes d’équivalence:

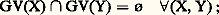– que cette décomposition met en évidence pour les systèmes fermés (ni entrées, ni sorties d’éléments) ou semi-ouverts (sorties mais non entrées d’éléments) des chaînes de filiation entre les classes susceptibles d’être occupées par les éléments du système, chaînes partant des GExV et aboutissant aux GEnV en passant éventuellement par des GMV (la figure 5 donne un exemple arbitraire de décomposition pour un système fermé); les GEnV et les GFV constituent les attracteurs du système, au sens de la dynamique qualitative;

– que les systèmes ouverts susceptibles d’atteindre un état stationnaire comportent des chaînes de GMV entre leurs entrées et leurs sorties (la figure 6 donne un exemple de décomposition pour un tel système);

– que ce type de décomposition permet de bien séparer les transformations réversibles au sens large (à l’intérieur d’une C.F.C.) et les transformations irréversibles (entre les C.F.C.).

Il est à noter que les propriétés qui viennent d’être rappelées sont très générales et valables pour les systèmes très divers qui relèvent de la représentation adoptée, indépendamment de la nature des éléments qui les constituent et du nombre de classes d’équivalence et d’arcs nécessaires à leur description. C’est bien là l’un des buts de toute théorie interdisciplinaire.

Forme générale des équations d’évolution

Si les données qualitatives que l’on peut extraire du graphe représentatif d’un système de transformations apportent déjà une première contribution importante à notre connaissance du système, il n’en reste pas moins que l’étude quantitative de celui-ci exige la mise en œuvre des équations d’évolution qui le régissent. Dans le cadre de l’axiomatique choisie, l’écriture de ces équations se fait simplement en utilisant les formes analytiques des fonctions de transformations définies par les axiomes 3, 4 et 5 et en explicitant le bilan instantané des entrées et sorties d’éléments dans chaque classe.

On obtiendra donc les équations différentielles d’un système quelconque en écrivant:

(j = 1 à n si le système comporte n classes).

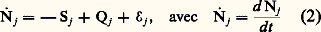– Le terme S^j représente la somme des sorties d’éléments de la classe E^j dépendant de l’occupation d’au moins une des classes du système:

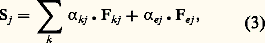où F^kj sont les sorties de E^j vers les autres classes E^k du système, et F^ej les sorties de E^j vers l’extérieur du système.

– Le terme Q^j représente la somme des entrées d’éléments dans E^j , dépendant de l’occupation d’au moins une des classes du système:

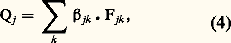où F^jk sont les entrées dans E^j à partir des autres classes E^k du système.

– Le terme 劉^j représente les entrées (face=F0021 劉^j 礪 0) ou sorties (face=F0021 劉^j 麗 0) d’éléments de E^j indépendantes de l’occupation des classes du système. Il peut s’agir aussi bien d’entrées commandées de l’extérieur que de sorties s’effectuant selon un processus particulier («effets de surface» relevant de l’axiome 7, par exemple).

On voit immédiatement que si certaines transformations relèvent de l’axiome 5, le système différentiel (2) sera non linéaire.

Si toutes les transformations relèvent seulement des axiomes 3 et 4, les fonctions F s’écrivent (cf. (1)) sous la forme la plus générale:

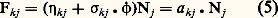et le système différentiel (2) est linéaire.

En vertu des mêmes axiomes 3 et 4, on remarque également que les situations linéaires impliquent que tous les coefficients 見^kj soient égaux à 1. Cela est une condition nécessaire mais non suffisante (on peut en effet avoir encore dans ce cas des termes du type F = K 練 N^j 練 N^{j +1}... relevant de l’axiome 5, donc non linéaires). Il faut donc, en outre, qu’il n’y ait pas d’arcs simultanés convergeant vers une classe quelconque (fig. 3). Mais il peut exister des arcs simultanés divergeant à partir d’une classe quelconque (fig. 2); on démontre d’ailleurs que ceux-ci sont alors situés obligatoirement, dans les systèmes linéaires, sur la frontière de graphes vrais (cf. P. Delattre, L’Évolution des systèmes moléculaires ).

En revanche, les coefficients 廓^jk peuvent être différents de 1, même dans les situations linéaires. Si au moins un 廓^jk est supérieur à 1, on aura alors un système linéaire multiplicatif; si tous les 廓^jk sont égaux à 1, le système linéaire sera dit non multiplicatif.

Dans les cas linéaires non multiplicatifs, on pourra finalement écrire les équations (2) sous la forme:

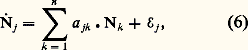avec la convention:

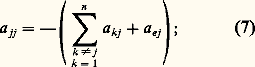les termes a ^jk (k j ) représenteront donc les entrées d’éléments dans E^j en provenance des autres classes du système, tandis que le terme a ^jj représentera les sorties d’éléments de E^j vers les autres classes du système (a ^kj pour j k ) ou vers l’extérieur du système (a ^ej ).

Finalement, l’ensemble des équations d’un système s’écrira dans ce cas linéaire sous la forme matricielle:

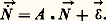Et la matrice A = [a ^jk ] aura la structure de signes bien définie suivante:

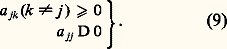Pour les systèmes linéaires multiplicatifs, le formalisme général reste le même, mais la matrice A de (8) s’écrit alors:

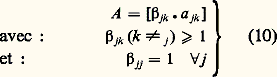puisque 廓^jj est associé à l’ensemble des sorties de E^j et que, pour toutes ces sorties, les coefficients 見 sont égaux à 1.

Nous allons résumer quelques-unes des propriétés des systèmes de transformations linéaires, particulièrement en ce qui concerne la forme générale de leurs solutions, et les valeurs propres qui y interviennent.

On sait que la solution du système (8) est de la forme:

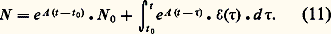Si 劉 = C ^te :

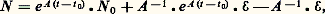t ⁰ étant l’instant initial (que l’on choisit généralement égal à zéro), et N ⁰ la matrice-colonne des états initiaux dans les différentes classes du système.

Si 劉 ne dépend pas du temps (entrées constantes sur les classes du système alimentées de l’extérieur), le système tend vers l’état stationnaire qui annule le second membre de (8):

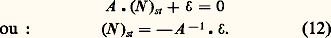Si 劉 est nul (système semi-ouvert; aucune entrée sur les différentes classes: 劉^j = 0 葉j ), la solution (11) se réduit à:

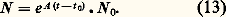Lorsque l’on explicite les solutions (11) ou (13), les fonctions exponentielles matricielles s’expriment en fonction des valeurs propres de A . Par exemple, si t ⁰ = 0, et si toutes les valeurs propres de A sont distinctes (¹,², ...,ⁿ si A est d’ordre n , c’est-à-dire si le système de transformations a n classes), on a:

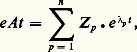avec, pour les matrices constituantes Z ^p :

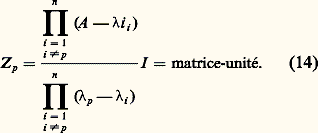Une solution telle que (13) donne donc finalement, pour le contenu N^j d’une classe E^j , en fonction du temps, une expression de la forme (lorsque les valeurs propres sont distinctes):

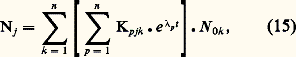K^pjk étant le terme situé dans la j -ième ligne et la k -ième colonne de la matrice constituante Z ^p correspondant à la valeur propre^p .

Liens entre la réductibilité de la matrice représentative et la décomposition du système en graphes vrais

Dans le cadre de l’axiomatique utilisée ici, il existe pour les systèmes de transformations linéaires un lien direct entre la décomposition en graphes vrais et la réductibilité de la matrice A . Ce lien est illustré par les figures 7 et 8. À chaque graphe vrai, considéré avec ses seules fonctions de sorties (et non d’entrées), correspond une sous-matrice centrée sur la diagonale principale de A . Les liaisons entre graphes vrais apparaissent dans le quadrant inférieur gauche de A , alors que le quadrant supérieur droit ne comporte, en dehors des sous-matrices centrées sur la diagonale principale, que des zéros.

Les arcs g ^pq correspondent aux liaisons entre des classes appartenant respectivement aux graphes vrais numérotés q et p .

– M ^p est la sous-matrice correspondant au graphe vrai numéroté p (avec seulement ses arcs de sortie dépendant de l’occupation de certaines classes);

– MT ^pq est la sous-matrice de transfert comportant les liaisons entre les graphes vrais numérotés q et p (MT ^pq contient donc les termes de A correspondant à l’arc g ^pq de la figure 8).

2. Un exemple d’application: la détermination des variables pertinentes pour les systèmes de transformations soumis à une action extérieure

Les actions extérieures sur un système de transformations sont symbolisées, d’une manière générale, par le facteur 﨏 introduit dans l’axiome 3. Nous avons vu que le «champ» ainsi représenté peut être de nature physique très diverse, selon les systèmes et les environnements considérés. Pour les systèmes biologiques, 﨏 correspond souvent soit à une concentration de substance nutritive ou toxique, soit à l’intensité d’un rayonnement électromagnétique ou particulaire. Un système donné peut, bien entendu, être soumis simultanément à l’action de plusieurs champs 﨏¹, 﨏², 﨏³... de natures physiques différentes.

La question que l’on se pose est de savoir quels sont les variables et paramètres qui doivent être choisis pour rendre compte, d’une manière théorique cohérente, des effets observés.

En réalité, le problème se pose parce que les expérimentateurs, qui ont effectué dans les domaines concernés des études de caractère plutôt empirique, ont souvent adopté comme variable de référence une grandeur, appelée dose D, équivalente au produit 﨏 練 t , ou plus généralement à l’intégrale:

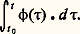Lorsque, dans les disciplines en question (radiobiologie, pharmacologie, toxicologie, etc.), les effets temporels ne sont pas passés sous silence, ils sont souvent considérés conjointement avec la dose D (qui contient déjà implicitement le temps), et sous la forme de facteurs correctifs à déterminer plus ou moins empiriquement. Il est beaucoup plus rare de voir séparer nettement 﨏 et t en faisant apparaître ces deux facteurs simultanément dans la théorie. Cette dernière manière de faire, qui est respectée dans le formalisme des systèmes de transformations, constitue une condition sine qua non si l’on veut pouvoir distinguer avec une rigueur suffisante les situations où 﨏 et t doivent entrer en ligne de compte séparément et les situations où le regroupement dans la variable composite D 黎 﨏t est admissible.

On remarquera que le fait d’avoir distingué explicitement 﨏 et t dans l’écriture des équations d’évolution des systèmes de transformations n’est pas une pétition de principe qui introduirait a priori la conclusion précédente, d’une façon arbitraire. Cette manière de faire résulte simplement d’une nécessité de cohérence rationnelle dans l’écriture des équations. En effet, puisque les premiers membres de ces équations représentent des variations différentielles en fonction du temps, les seconds membres doivent s’exprimer sous la forme de termes correspondant à des actions instantanées sur le système (c’est-à-dire de termes en 﨏 s’il s’agit des actions du champ d’intensité 﨏). Introduire dans ces termes des facteurs intégraux tels que D correspondrait à des phénomènes très particuliers, dont l’existence devrait être démontrée a posteriori, et non posée a priori.

Cette position fondamentale étant étayée, voyons maintenant comment aborder l’analyse des situations où l’emploi de la variable de référence intégrale D 黎 﨏t est ou n’est pas justifiée. Cette analyse relève d’abord d’une première critique générale d’ordre qualitatif sur l’usage de D, faisant appel aux conséquences des deux premiers axiomes des systèmes de transformations. Puis, à l’aide du formalisme analytique décrit précédemment, une seconde critique plus précise peut être développée et permet de distinguer de manière très nette (par démonstration) les situations où D peut servir, ou non, de variable de référence (cf. P. Delattre, L’Évolution des systèmes moléculaires , in General Systems Yearbook et in Biological and Environmental Effects of Low-Level Radiation ).

Première critique. Nous utiliserons ici le principe de décomposition des systèmes de transformations en graphes vrais, tels qu’il a été décrit au chapitre Représentation sous forme de graphes. À titre d’exemple illustratif, supposons que nous ayons affaire au système de la figure 9, où sont représentées en traits gras les transformations provoquées par le champ 﨏 (fonctions f ^jk relevant de l’axiome 3) et en traits fins les transformations spontanées (fonctions g ^jk relevant de l’axiome 4). Le concept de dose globale reçue par le système pour une action donnée du champ correspond à une sommation arithmétique de toutes les absorptions associées aux fonctions f ^jk . Or il est facile de constater que ces diverses fonctions n’ont pas la même signification qualitative, eu égard à l’évolution du système; leur sommation pure et simple revient donc à additionner des quantités hétérogènes. Pour comparer les rôles que jouent les diverses fonctions f ^jk , il suffit d’examiner comment leur présence ou leur absence modifie l’évolution qualitative du système. Voyons, par exemple, ce qu’il en est pour les fonctions f ⁴¹, f ⁴³, f ⁵⁴:

– la présence ou l’absence de f ⁴¹ ne modifie par la connexité du GExV1; dans les deux cas, le système tend vers une structure d’équilibre qui est celle du GEnV3;

– la fonction f ⁴³ n’est pas aussi «neutre»: lorsqu’elle est présente, le système tend vers la structure de GEnV3; lorsqu’elle est absente, la classe E³ constitue à elle seule un second GEnV qui subsistera dans l’état d’équilibre final, conjointement avec GEnV3;

– la fonction f ⁵⁴ joue un rôle encore plus important: sa présence entraîne la situation d’équilibre définie par le GEnV3; son absence fait que le GExV1 devient un graphe fermé qui subsistera tel quel dans l’état d’équilibre vers lequel tend le système.

Ainsi les trois fonctions considérées jouent des rôles qualitatifs suffisamment différents pour que la validité de leur assimilation dans la dose globale soit mise en cause.

Supposons maintenant que les effets dont on veut rendre compte ne concernent pas la totalité des classes du système, mais seulement une ou plusieurs classe(s) du GMV2. On sait que l’évolution de ces classes dépend de la structure et des fonctions de transfert de ce GMV2, ainsi que du GExV1 situé dans son ascendance, mais en aucune manière de ce qui définit le GEnV3, puisque celui-ci est situé dans la descendance des classes considérées. Rapporter les effets étudiés à la dose totale reçue par le système, qui inclut les absorptions correspondant à toutes les fonctions f ^jk , revient donc à prendre pour référence une grandeur qui englobe indifféremment des phénomènes agissant en tant que cause des effets observés et des phénomènes qui ne jouent aucun rôle dans ces effets. Il est clair que, dans ce cas, tenter d’établir une théorie des effets en fonction de la dose globale D ne peut qu’être une opération vouée généralement à l’échec.

Seconde critique . La conclusion qui vient d’être énoncée peut être démontrée d’une manière générale, indépendamment même des relations ascendance-descendance dont il a été question ci-dessus, et en considérant seulement l’existence simultanée de transformations dues à un champ 﨏 et de transformations spontanées. Il suffit pour cela de considérer les équations d’évolution des systèmes de transformations dans le cas linéaire le plus simple, où interviennent simultanément ces deux types de transformations (axiomes 3 et 4), les conclusions devant rester a fortiori valables dans les situations plus complexes, par exemple lorsque existent des transformations non linéaires relevant de l’axiome 5 (qui ne dépendent pas du champ 﨏, comme pour l’axiome 4).

Soit donc un système obéissant à l’équation matricielle:

où le terme général de la matrice A s’écrit: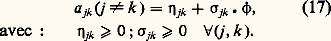

L’effet e que l’on veut étudier est toujours lié à certains états occupés par les éléments constitutifs du système, ce qui signifie que e est une fonction h des taux d’occupation N^j , N^p , N^q ... d’un certain nombre de classes d’équivalence E^j , E^p , E^q ... du système:

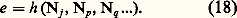Les variables et paramètres pertinents devant permettre de faire la théorie des effets e sont donc ceux en fonction desquels s’expriment les contenus N^j , N^p , N^q ... des classes concernées. Or ces contenus de classes s’écrivent d’une manière générale sous la forme (15) (cf. supra , Forme générale des équations d’évolution ), où, rappelons-le, le coefficient K^pjk est le terme situé dans la j -ième ligne et la k -ième colonne de la matrice constituante Z ^p correspondant à la valeur propre^p ; cette matrice constituante s’écrivant, lorsque toutes les valeurs propres de A sont distinctes, sous la forme (14) (cf. supra , Forme générale des équations d’évolution ). Les sommations de 1 à n dans les expressions (14) et (15) correspondent au système ou sous-système des n classes qui conditionnent l’effet e considéré, compte tenu des relations d’ascendance-descendance dont il a été question plus haut.

Par ailleurs, les valeurs propres^p sont les solutions de l’équation caractéristique:

Les coefficients de cette équation algébrique font intervenir des produits et sommes diverses des termes de la matrice A , ces termes étant de la forme (17). Les coefficients de l’équation caractéristique comporteront donc, en général, des termes constants et des termes en 﨏 élevés à des puissances diverses. En définitive, les valeurs propres^p , qui sont exprimables en fonction des coefficients de l’équation caractéristique (dans le cas général, sous la forme de fonctions hypergéométriques, cf. G. Belardinelli), correspondront donc à des expressions où 﨏 apparaît à des puissances diverses: les^p sont équivalents à des expressions contenant des termes en 﨏, 﨏², ..., 﨏^x . Le même raisonnement est applicable aux termes résultant des produits de matrices (A 漣ⁱ I ) qui interviennent dans Z ^p (relation (14)). Les coefficients K^pjk correspondront donc également à des expressions où 﨏 apparaît à des puissances diverses: les K^pjk sont équivalents à des expressions contenant des termes en 﨏, 﨏², ..., 﨏^y .

En définitive, on peut dire que les N^j (15), et par conséquent les effets e (18), relèvent d’expressions où interviennent des coefficients K exprimables en 﨏, 﨏², ..., 﨏^y et des arguments d’exponentielles^p t exprimables en 﨏t , 﨏²t , ..., 﨏^x t . Il en ressort qu’une théorie des effets e n’est pas en général possible en fonction de la seule variable composite D 黎 﨏t . Si l’on voulait utiliser cette variable, il faudrait simultanément faire intervenir le temps à des puissances diverses puisque: dans les K^pjk , les 﨏^y correspondraient à des termes D^y 練 t ^-y ; dans les^p t , les 﨏^x t correspondraient à des termes D^x 練 t ^1-x ; ce serait une méthode assez barbare, et pratiquement inexploitable. Il est évidemment bien plus logique de séparer systématiquement 﨏 et t , le temps étant une variable indépendante et l’intensité 﨏 du champ, un paramètre.

Voyons maintenant si une théorie en termes de D est cependant possible dans certains cas particuliers. Supposons que toutes les transformations dépendent uniquement du champ 﨏. Le terme général de la matrice A s’écrit dans ce cas:

et, par conséquent:

la matrice A ne contenant plus que les termes 靖^jk .

Pour étudier l’équation caractéristique (19), faisons le changement de variable:

l’équation (19) s’écrit maintenant: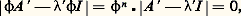

c’est-à-dire, pour 﨏 0:

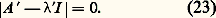Les ^p , racines de (23), sont donc des constantes puisque A est constante:

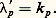On en déduit, en vertu de (22):

Les valeurs propres de la matrice A sont donc toutes proportionnelles à 﨏. Par ailleurs, les matrices constituantes Z ^p s’écrivent maintenant: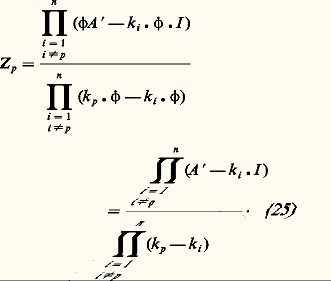

Les termes K^pjk de ces matrices constituantes sont donc maintenant constants. Il en ressort que les expressions (15) et (18) sont exprimables à l’aide de termes où 﨏 et t interviennent seulement dans les arguments des exponentielles et sous la forme:

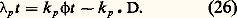Une théorie des effets en fonction de la dose D est alors possible, quelle que soit la complexité du système considéré. On doit toutefois ajouter que ce cas particulier, où toutes les transformations du système dépendent du champ 﨏, et où il n’existe aucune transformation spontanée, ne peut être qu’extrêmement rare en pratique. Tout système physique, et a fortiori biologique, réagit aux actions extérieures dues, par exemple, à des rayonnements ou à des substances chimiques (désexcitations atomiques ou moléculaires, recombinaisons, restaurations, etc.). En outre, dans le cas des systèmes biologiques, la cinétique métabolique propre des objets étudiés, indépendamment même des réactions aux atteintes particulières que l’on considère, subsiste et se combine à ces réactions, et participe par conséquent à la réponse globale que l’on observe. Il existe donc en général, dans les systèmes étudiés, des transformations «spontanées» relevant de l’axiome 4, ce qui exclut la possibilité d’une théorie des effets en fonction de la seule «dose».

Encyclopédie Universelle. 2012.